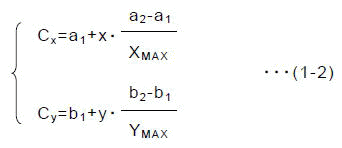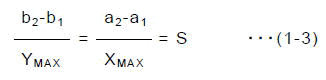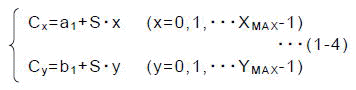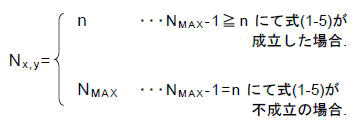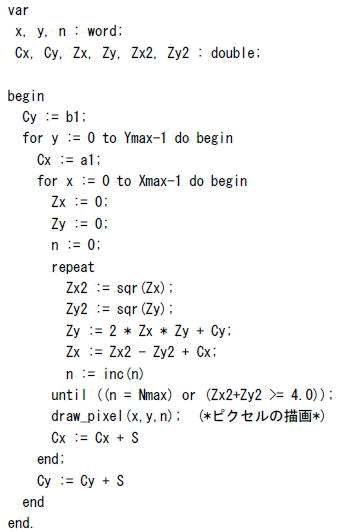|
まずこの章では,Mandelbrot集合のコンピュータグラフィックスについて説明し,従来の方法,すなわちソフトウエアによる描画法とその問題点について述べます.そして,ハードウエアによる解決法としてのPyxisの,内容説明への導入とします.
1.1 対象
フラクタル図形の代表として有名なものに,Mandelbrot集合(以下M集合)のコンピュータグラフィックス(CG)があります.この不可思議な形状には,文字どおりの
"無限" が醸し出す想像を超えた美しさ,神秘性が潜んでいます.従来より多数の書籍,雑誌の中で紹介されているほか,それらのCGばかりを集めた本が出版されていることからも,その不思議な魅力にとりつかれた人の多さが想像できます.
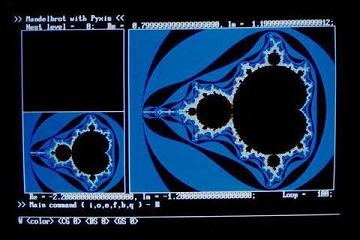
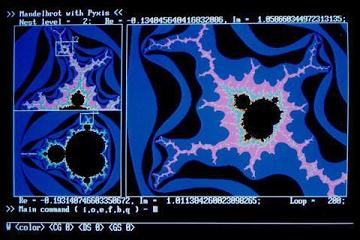
写真1-1から写真1-7は,Pyxisを用いた描画画面の例です.写真1-1はM集合の全体像,写真1-2以降は全体像の一部を拡大描画したものです.
|
 [写真1-1] [写真1-1]
M集合の全体像.
水色で囲まれた,黒い横倒しの雪だるま形状の部分がM集合.
描画対象領域の左下と右上の点の座標がそれぞれ表示されている.
|
|
 [写真1-2] [写真1-2]
M集合上部を拡大したところ.細いヒゲの中に,全体と自己相似な図形があることがわかる.
左の小さい枠内には,拡大した範囲が表示されている. M集合の全体像.
|
|
 [写真1-3] [写真1-3]
雪だるまの首部の拡大.
周囲にも,全体とよく似た形状が無限に付随していると想像できる.
|
|
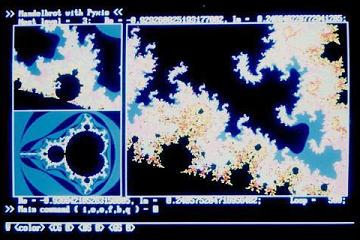 [写真1-4] [写真1-4]
写真1-3の一部をさらに拡大.
|
|
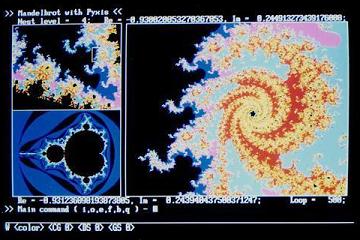 [写真1-5] [写真1-5]
写真1-4の一部をさらに拡大.
大きな,無限に続く渦が現れる.
|
|
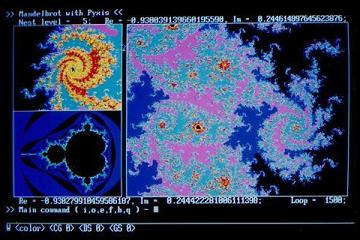 [写真1-6] [写真1-6]
写真1-5の,渦の一部をさらに拡大.
渦の中は非常に複雑な乱流になっている.
|
|
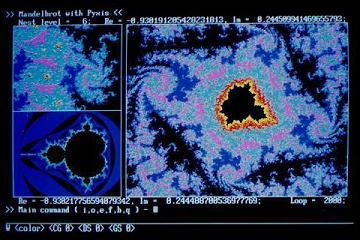 [写真1-7] [写真1-7]
写真1-6の一部をさらに拡大.
乱流の中から,本体と自己相似な図形が現れた.その周囲には,複雑ながらも整然とした無限の自己相似図形が集まって,デザイン化された模様のようになっている.
|
ここで,M集合とその描画について簡単に説明しておきます.
Zを複素変数,Cを複素定数として,次式
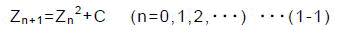
をZ0=0として反復演算します.この結果,反復回数nを無限大としても|Z|が無限に大きくならないCの集合がM集合です.基本となるルールは,驚くべきことにたったこれだけです.
これを画面に描画します.描画法にも種々あるようですが,ここではもっとも一般的と思われる方法について説明します.
|
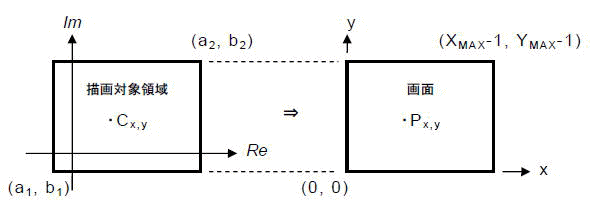
[図1-1]複素平面内の描画対象領域と表示画面
|
図1-1のように,複素平面内に,ある描画対象領域(a1,b1)-(a2,b2)を考え,これを画面に当てはめます.画面のサイズ(ピクセル数)をXMAX×YMAX,その中の画面座標(x,y)のピクセルをPx,yで表すとします.さらに,各Px,yに対応する描画対象領域内の点をCx,yとして,これは
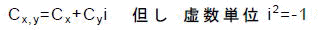
であるとすれば,Cx,Cyは,
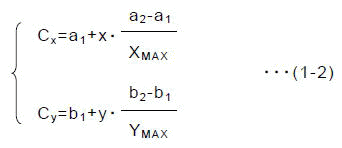
さらに,画像の変形をさけるため,x軸とy軸のスケールが等しくなるように,
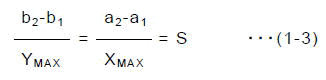
と置き換えれば,式(1-2)は,
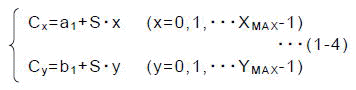
となります.
ところで,実際の演算では無限大を扱うことはできませんから,|Z|とnのそれぞれに対して,無限大とみなすための閾値を設定します.式(1-1)の反復において,あるnの時点で

が満たされれば,それ以降の反復により|Z|は無限に大きくなりますので,これを判定基準とします1).またnについては,描画結果と描画時間との兼ね合いにより,予め適当な最大反復回数NMAXを設定しておくものとします.
さて,式(1-4)のCx,yを式(1-1)のCとして反復演算を行います.そしてNMAX回までの反復の中で,毎nにつき式(1-5)が満たされるか否かを調べていきます.
反復はn=NMAX-1か式(1-5)の成立にて終了とします.そして,その時のnの値を演算結果とします.これをNx,yとすると,すなわち
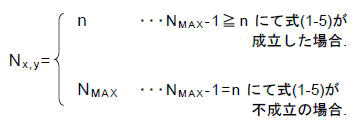
この結果に基づき,画面上の1ピクセルPx,yを描画します.Nx,y=NMAX-1ならば黒で描画し,Nx,y<NMAX-1ならばNx,yの値を使って適当な色で描画します.
以上の処理をx,yすべての組み合わせについて行えば,1画面分の描画図形が得られます.そこでは,M集合の部分は黒で,そしてそれ以外の部分には,Zが無限遠点へ飛び去る速さの違いが色のパターンとなって表現されることになります.
このようにして,様々な対象領域Cに対する画像を得ることが,M集合のCGの目的となります.
(注)筆者が使用しているコンピュータは色数が少ないため,M集合以外の部分にも黒を使用しています.画面写真参照の際,注意してください.
1.2 問題点
以上の処理をソフトウエアで実現するのは簡単です(リスト1-1参照).しかし,問題は演算量です.
ZもCと同様に
で表されるとすると,Zの反復1回に含まれる演算は,リスト1-1に注意しつつ,式(1-1)より

となりますから,最低8回の浮動小数点加減乗算が必要です.例えば,
XMAX=400,YMAX=320,NMAX=100
として,すべてのピクセルがM集合に含まれる場合(NMAX回反復する)を考えると,仮に判定用比較演算や,また正規化,加減算時の桁合わせなどを考えないとしても,演算量は1億回を越えます.これを例えば1分以内に描画するには,最低限約2MFLOPSの性能が必要になります.
今でこそ32ビットMPUやオンチップFPU,浮動小数点演算DSPなどが当たり前になっていますが,当時(1986年頃)はまだ8ビットマシンを使っている人も多かった頃で,1枚の画面を得るのに一晩かかるのが普通でした.PC98XL2(386+387)でも数時間,筆者の使っていた自作CP/Mマシンでは十数時間も必要でした.これでは,「この辺を拡大するとどうなっているのだろう」と思っても,結果がでるのは翌日です.これは精神衛生上,非常によくありません.
|
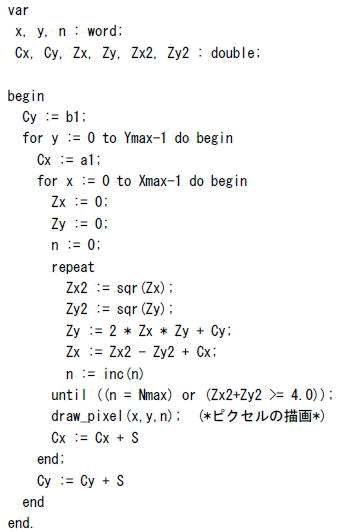
[リスト1-1]M集合の描画処理例
|
1.3 解決法
もちろん,高価なハードウエアを用意すればすぐにでも高速化はできますが,それでは面白くありません.そこで,専用ハードウエア(Pyxis)を自作することにしました.当時筆者は貧乏学生だったので,予算を労力でカバーすることを基本方針としました.
では,2章以降で本論に入ります.Pyxisは回路規模が大きく,動作も複雑ですので,本レポートの説明は考え方を中心に進めたいと思います.
1.4 略記号について
本レポートでは説明簡略のため略記号を多用します.以下に主なものを挙げておきますので適宜参照してください.
|
a1
b1
C
Cx,y
Cx
Cy
CKPA
LE
LD
n
Nx,y
NMAX
|
:描画対象領域実軸原点
:描画対象領域虚軸原点
:式(1-1)における複素定数
:Px,yに対応するC
:Cx,yの実数成分
:Cx,yの虚数成分
:部分積加算クロック
:PE用結果レジスタ
:PD用結果レジスタ
:式(1-1)における反復回数
:Px,yについての演算結果
:最大反復回数
|
|
Px,y
PE
PD
S
XMAX
YMAX
Z
Zx
Zy
Znx
Zny
|
:画面座標(x,y)のピクセル
:ピクセルペアの内xが偶数のピクセル
:ピクセルペアの内xが奇数のピクセル
:1ピクセルに対応する複素平面上の幅
:描画画面のx方向のピクセル数
:描画画面のy方向のピクセル数
:式(1-1)における複素変数
:Zの実数成分
:Zの虚数成分
:nを意識したZx
:nを意識したZy
|
|
 [写真1-1]
[写真1-1] [写真1-2]
[写真1-2] [写真1-3]
[写真1-3] [写真1-4]
[写真1-4] [写真1-5]
[写真1-5] [写真1-6]
[写真1-6] [写真1-7]
[写真1-7]