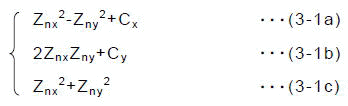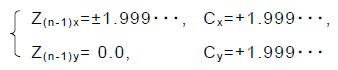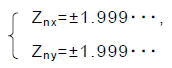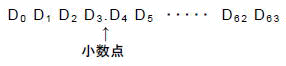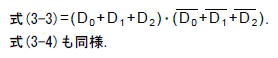|
|
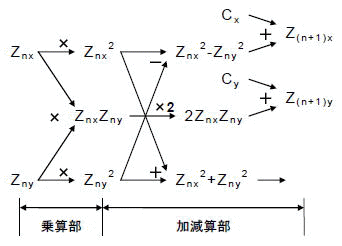
[図3-1]演算フロー
|
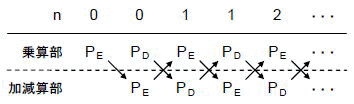
[図3-2]パイプラインとピクセルペア
|
3.1 演算フローの検討
式(1-6)及びリスト1-1をデータフローを中心に考えると,図3-1のように表すことができます.
(1)パイプライン化
この図から,反復1回分の演算は前半の乗算部と後半の加減算部に分割でき,かつそのそれぞれが,互いの演算結果を利用し合う形のループになっていることがわかります.よって,乗算部と加減算部をパイプライン化することで,それぞれを休むことなく動作させることができます.そのため,このパイプラインループに2ピクセル分のデータをいれ,乗算部と加減算部を交互に回るように全体を構成しました.
まずPEが乗算部へ入り,その結果が加減算部へ送られると同時に乗算部ではPDの処理が開始されます(図3-2).以後これを反復し,PEが乗算部に戻ってくる毎にnが1増えることになります.
このように,PE,PDのそれぞれについて式(1-1)の反復演算が同時に行われます.これにより通常動作中の演算回路の利用効率を100%とすることができます.
(2)並列処理
図3-1のフローには乗算Znx2,ZnxZny,Zny2を中心とした,次の3つの大きな流れがあることがわかります.
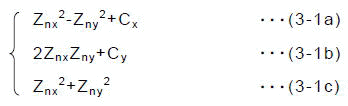
これらはそれぞれ,式(1-6a)の実部と虚部,式(1-6b)に対応しています.
主な演算部を,この乗算を中心とした3つに分解し,その各部が並列に動作するようにしました.乗算器を3つ用意し,そのそれぞれから同時に出力される結果を,3分割された各加減算部が並列に利用しています. なお式(3-1b)の2倍演算は,ZnxZnyの乗算結果をステージ間レジスタにロードする部分で1ビットずらしておくことで処理しています.
以上のように,演算フローの中の並列性を,コスト他の制限が許す範囲で最大限に利用しています.それによって,全体の処理速度,演算回路の利用効率をそれぞれ向上させています.
3.2 数値のデータ表現
演算数値データのフォーマットは,2の補数固定小数点64ビットにしました.ビット割り当ては,符号1ビット,整数部3ビット,小数部60ビットです.
(1)ビット配分
式(1-5)の条件により,M集合の演算は実数部虚数部ともに±2の範囲で考えれば十分です.これを有効利用すれば,無用に大きな数を表現する必要がなくなり,整数部のビット数を最小限に押さえられます.実際には,式(1-5)の判定をZx2+Zy2だけでなく,それぞれ2乗する前のZx,Zyにおいても判定するようにして,整数部を3ビットに押さえています.これについては次項で説明します.
(2)2の補数表現
Pyxisの乗算回路には,2の補数をそのまま乗算できる2次Boothアルゴリズムを用いています.これにより,演算回路のすべてでデータ表現を2の補数に統一することができます.符号反転や絶対値などの余分な回路を省略し,かつ加減算と相性の良い最適な表現法といえます.
(3)ビット数と固定小数点表現
データ長に64ビット用意したのは,非常に大きな拡大率の図形に対して十分な反復回数の演算ができるようにするためです.この固定小数点表現なら有効桁は十進数で18桁以上ありますので,対象の複素平面に対して一様(これが重要)に十分な精度が得られます.浮動小数点方式では,表現できる数値が対数的であることに加え,1.0付近の数値を表現すると指数部が無意味になることから,ハードウエアが複雑になる以上にそのメリットはありません.
3.3 式(1-5)の判定法
(1)Znx2+Zny2の判定
|Zn|を得るためには(Znx2+Zny2)1/2を計算する必要がありますが,式(1-5)の判定が目的ならもちろんこれは不要で,次式の成立を調べれば十分です.
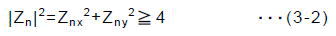
(2)判定法の改良
しかし,3.2で説明したように,64ビットの数値データを有効に使うためには,できるだけ小数部のビット数が多い方が有利です.
仮に,あるn-1回目における式(3-2)の判定が
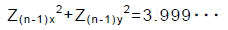
にて不成立となったとすると,次回(n)の判定の時には,例えば,
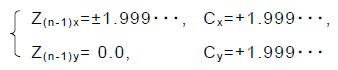
の時に,
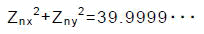
となってしまいます.この数を表せるようにするには,整数部に6ビットが必要です.
このビット数を削減するため,2乗の前のZnx,Znyをそれぞれチェックする回路を追加しました.もちろんこのためのハードウエア量が大きければ本末転倒ですが,論理的にはわずかゲート3個で実現可能です.
式(3-1)において,

のいずれかが成り立つならば,式(3-2)も成立します.
この式(3-3),式(3-4)の判定を,Znx,Znyが乗算部に入る直前に行います.このことは,式(3-2)の評価の一部を1反復サイクル前に先取りして行うことと同じです.従って,式(3-3),式(3-4)の判定結果は制御回路にて1サイクル分遅延した後,式(3-2)と併せて評価するようにします.
これによるワーストケースは,式(3-3),式(3-4)のどちらもを満たさない最大値,
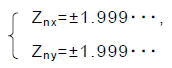
の場合で,
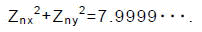
以上より,式(3-3),式(3-4)の判定を加えることで,整数部のビット数を3ビットに押さえながら,式(1-5)の正確な判定が可能になります.
(3)実際の判定法
ここでは,数値データをビット展開して,次のように表現します.
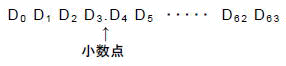
(a)式(3-2)の判定
判定基準は正数で4以上ですから簡単です.
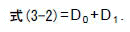
(b)式(3-3),(3-4)の判定
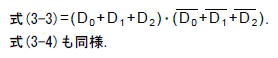
このように,簡単な論理回路にて判定が可能です.
○ここまでで,構成,機能,動作,方法を,それぞれ抽象的な表現を中心に概説しました.次の章からは,これらがどのように具体化されているかの解説に移ります.まず全体のブロックダイヤグラムを示し,その中の構成要素を順に説明していきます.
|